Para calcular la intersección de una recta y un plano, se pasa un plano por la recta, calculamos la recta de intersección de los 2 planos. Ésta recta corta a la dada en un punto y es el de intersección.
Si dos rectas se cortan determinan un plano, por lo que sus trazas están en las rectas de un plano. Si dos rectas se cortan, el punto de intersección de ambas tiene sus proyecciones alineadas en planta y alzado sobre una vertical. Si no están alineadas las proyecciones del punto sobre una vertical, las rectas se cruzan.
La intersección de dos planos queda determinada por la intersección de sus trazas. La recta que pasa por esos dos puntos es la recta de intersección de los mismos.
Intersección de recta y plano
Dada la recta oblicua y plano oblicuo beta, se pasa un plano cualquiera por la recta r (en este caso uno vertical), la recta de intersección de los 2 planos determina en el alzado el punto de intersección A2 con la recta , sólo hay que bajar su proyección A1 a la planta.


Intersección de recta y plano. Para calcular la intersección de la recta a y el plano beta, pasamos un plano auxiliar alfa por a. Los dos planos verticales se cortan en una recta vertical que corta a la recta a en el punto P.


Intersección de planos
Intersección de plano verde y rojo. Una recta queda determinada por dos puntos y la intersección de las trazas horizontales y verticales de los dos planos son dos puntos por donde pasa la recta de intersección BC. Si utilizamos el plano de perfil tenemos otras dos trazas de los planos que se cortarán en un punto A de la misma recta de intersección BC.


Los puntos de intersección de las trazas en planta y alzado determinan la recta r de intersección de los dos planos.


Intersección de un plano vertical y oblicuo. La recta a la determinan los dos puntos de intersección de las trazas de los planos.


Intersección de un plano vertical y oblicuo en sistema diédrico. La recta r la determinan los dos puntos de intersección de las trazas de los planos alfa y beta.

La recta a de intersección de los dos planos tendrá sus 3 trazas HA VA Pa en las 3 trazas de los planos por pertenecer a ambos.


Si un plano beta es cortado por uno paralelo a los de proyección (PH) su intersección a es paralela a la traza correspondiente.

En la figura un plano horizontal beta (paralelo al PH) corta a uno oblicuo alfa. La recta de intersección r1 es por tanto paralela a alfa1.

Un plano vertical v y otro proyectante vertical o de canto c se cortan según una recta oblicua a. Las trazas de los planos se cortan en el primer y cuarto cuadrante (Ha Va).


Dos planos se cortan en el segundo cuadrante según la recta i. Las proyecciones i1 i2 quedan por tanto sobre el 2º cuadrante.


Dos planos alfa beta se cortan en la intersección de las trazas, como las trazas horizontales son paralelas, la recta de intersección será una recta paralela a ellas ya que las tres se han de cortar en el mismo punto, esto es, en el infinito. La única recta que lleva dirección en el alzado hacia el infinito es aquella que es paralela a la línea de tierra.


Dos planos se cortan según el punto M en el primer cuadrante, desconociéndose su recta de intersección. Se hace un plano auxiliar, por ejemplo horizontal para que sus intersecciones a b con los planos dados sean paralelas a las trazas horizontales de los planos dados. Como a b son rectas de ambos planos y al mismo tiempo del mismo plano horizontal se cortan en un punto P por donde pasa la recta de intersección MP de ambos planos.




En la figura un plano horizontal beta (paralelo al PH) corta a uno oblicuo alfa. La recta de intersección r1 es por tanto paralela a alfa1.

Un plano vertical v y otro proyectante vertical o de canto c se cortan según una recta oblicua a. Las trazas de los planos se cortan en el primer y cuarto cuadrante (Ha Va).


Dos planos se cortan en el segundo cuadrante según la recta i. Las proyecciones i1 i2 quedan por tanto sobre el 2º cuadrante.


Dos planos alfa beta se cortan en la intersección de las trazas, como las trazas horizontales son paralelas, la recta de intersección será una recta paralela a ellas ya que las tres se han de cortar en el mismo punto, esto es, en el infinito. La única recta que lleva dirección en el alzado hacia el infinito es aquella que es paralela a la línea de tierra.


Dos planos se cortan según el punto M en el primer cuadrante, desconociéndose su recta de intersección. Se hace un plano auxiliar, por ejemplo horizontal para que sus intersecciones a b con los planos dados sean paralelas a las trazas horizontales de los planos dados. Como a b son rectas de ambos planos y al mismo tiempo del mismo plano horizontal se cortan en un punto P por donde pasa la recta de intersección MP de ambos planos.



Un plano phi oblicuo se interseca con uno frontal beta (paralelo al vertical). La recta de intersección en alzado (r2) es paralela a phi2, pues planos paralelos producen rectas de intersección paralelas y el frontal es paralelo al vertical.


Intersección de un plano beta paralelo a la línea de tierra y un plano oblicuo a.
La recta de intersección pasa por la intersección de las trazas.


La intersección de plano de canto (proyectante vertical) y oblicuo es una recta oblicua.


Intersección de plano paralelo a la línea de tierra y oblicuo con su recta oblicua de intersección.


Intersección de dos planos oblicuos.


Intersección de plano paralelo a la línea de tierra y oblicuo.


Intersección de plano de perfil beta y oblicuo alfa. Como el de perfil es paralelo al plano de perfil de proyección, la intersección a3 es paralela a la traza del plano alfa.




Intersección de un plano beta paralelo a la línea de tierra y un plano oblicuo a.
La recta de intersección pasa por la intersección de las trazas.


La intersección de plano de canto (proyectante vertical) y oblicuo es una recta oblicua.


Intersección de plano paralelo a la línea de tierra y oblicuo con su recta oblicua de intersección.


Intersección de dos planos oblicuos.


Intersección de plano paralelo a la línea de tierra y oblicuo.


Intersección de plano de perfil beta y oblicuo alfa. Como el de perfil es paralelo al plano de perfil de proyección, la intersección a3 es paralela a la traza del plano alfa.


Intersección de plano de perfil y oblicuo. La intersección de las trazas verticales de los planos queda en el cuarto cuadrante.


Intersección de plano definido por dos rectas m n y recta r.
Se hace un plano aleatorio beta incidente en r, éste corta a m n en AB. La recta AB corta a r en P, solución del ejercicio.

Intersección de dos planos paralelos a la línea de tierra (alfa y beta). Se proyecta el perfil de los elementos y se observa el punto de corte de las trazas de los planos en la tercera proyección. La recta de intersección r pasa por ese punto y es paralela a la línea de tierra.


Intersección de plano oblicuo y plano que pasa por la línea de tierra. La recta común a los planos es una recta que pasa por la línea de tierra y que pasa por el punto común de las trazas alfa 1 y alfa 2 y por el punto de intersección de alfa 3 y beta 3.


Intersección de dos planos oblicuos. Las dos trazas verticales se cortan en Vr y las horizontales en Hr y éstas son las trazas de la recta de intersección r.

Intersección de plano horizontal y oblicuo. Como el horizontal es paralelo al plano de proyección horizontal, su intersección será una recta horizontal r que pase por el punto de intersección P1 de las dos trazas verticales de los planos.

Intersección de plano frontal y oblicuo. Como el frontal es paralelo al plano vertical de proyección, tenemos el mismo ejercicio que el anterior, pero girado 180º (la planta pasa a ser alzado y recíprocamente).

Intersección de rectas
Si dos rectas se cortan están en un plano (por tanto las trazas de las rectas están en las trazas del plano) el punto de intersección de ambas tiene sus proyecciones en planta y alzado alineadas sobre una vertical en planta y alzado (ya que esta es la representación de un punto en sistema diédrico).

Las dos rectas sobre un plano con sus trazas sobre las de los planos.

A la izquierda dos rectas que se cortan con el punto de intersección alineado en una vertical en planta y alzado, ya que ésta es la posición de un punto siempre en diédrico.


Intersección de plano definido por dos rectas m n y recta r.
Se hace un plano aleatorio beta incidente en r, éste corta a m n en AB. La recta AB corta a r en P, solución del ejercicio.

Intersección de dos planos paralelos a la línea de tierra (alfa y beta). Se proyecta el perfil de los elementos y se observa el punto de corte de las trazas de los planos en la tercera proyección. La recta de intersección r pasa por ese punto y es paralela a la línea de tierra.


Intersección de plano oblicuo y plano que pasa por la línea de tierra. La recta común a los planos es una recta que pasa por la línea de tierra y que pasa por el punto común de las trazas alfa 1 y alfa 2 y por el punto de intersección de alfa 3 y beta 3.


Intersección de dos planos oblicuos. Las dos trazas verticales se cortan en Vr y las horizontales en Hr y éstas son las trazas de la recta de intersección r.

Intersección de plano horizontal y oblicuo. Como el horizontal es paralelo al plano de proyección horizontal, su intersección será una recta horizontal r que pase por el punto de intersección P1 de las dos trazas verticales de los planos.

Intersección de plano frontal y oblicuo. Como el frontal es paralelo al plano vertical de proyección, tenemos el mismo ejercicio que el anterior, pero girado 180º (la planta pasa a ser alzado y recíprocamente).

Intersección de rectas
Si dos rectas se cortan están en un plano (por tanto las trazas de las rectas están en las trazas del plano) el punto de intersección de ambas tiene sus proyecciones en planta y alzado alineadas sobre una vertical en planta y alzado (ya que esta es la representación de un punto en sistema diédrico).

Las dos rectas sobre un plano con sus trazas sobre las de los planos.

A la izquierda dos rectas que se cortan con el punto de intersección alineado en una vertical en planta y alzado, ya que ésta es la posición de un punto siempre en diédrico.
A la derecha dos rectas que no se cortan (se cruzan) pues P1 P2 no están alineados en la vertical, como sucedería en la representación de cualquier punto.


Los dos planos g j se cortan en una recta a que pasa por el segundo, tercero y cuarto cuadrante. Para determinar la intersección de ambos, prolongamos las trazas horizontales de ambos y obtenemos el punto de intersección P sobre el plano horizontal.
Prolongamos las trazas verticales de los planos hasta que se cortan en el punto O sobre el plano vertical. La recta que pasa por ambos puntos es la de intersección de los dos planos. Si representamos la tercera proyección en el perfil podemos observar que la intersección de las dos trazas determina M. Los 3 puntos POM, por pertenecer a ambos planos y estar en la recta de intersección están alineados.

Tenemos los dos planos g j de color azul determinados por las trazas g1 g2 j1 j2. Prolongamos la traza horizontal g1 del plano g hasta que corta a la traza horizontal j1 del plano j, obteniendo un punto de intersección P1 sobre el plano horizontal.
Prolongamos las trazas verticales de ambos planos g2 j2 y en su intersección O2 obtenemos un punto de la recta de intersección a sobre el plano vertical. Este punto O2 lo proyectamos sobre el perfil obteniendo O3.
Tenemos que la recta pasa sobre el plano horizontal por P1 y por el plano vertical por O2, proyectamos estos puntos sobre la línea de tierra obtenemos P2 O2, respectivamente. Los proyectamos también sobre el perfil para obtener la tercera proyección de los mismos P3 O3. La recta de intersección en su proyección horizontal a1 pasa por los puntos P1 O1, en su proyección vertical pasa por los puntos P2 O2. En su proyección en el perfil pasa por O3 y por el punto final del segmento d2, que es igual al alejamiento d1, esto es, la distancia del punto P1 al plano vertical.
De esta manera tenemos las tres proyecciones de la recta a (en el dibujo aparecen en color rojo), recta que pasa por el segundo, tercero y cuarto cuadrante.
Intersección de 2 figuras planas
Para calcular la intersección de dos triángulos se hace uso de un plano auxiliar horizontal alfa que los corta según las rectas a b, la intersección M de a b es un punto de la línea de intersección de los dos triángulos.

Operando de igual forma con otro plano beta, corta a los triángulos en c d , la intersección de c d es N.
MN es por tanto la recta de intersección de los dos planos.

El plano horizontal de mayor cota corta al triángulo amarillo según AB, al rojo según MN, la intersección de AB y MN es I. Bajamos las proyecciones de A2, B2, M2,…al contorno de los triángulos en planta, obteniendo A1, B1,…etc.
El plano horizontal de menor cota corta al triángulo amarillo según KL, al rojo según YZ, la intersección de KL e YZ es J. Bajamos igualmente las proyecciones de estos puntos a la planta.
La recta YJ es la intersección de los dos triángulos. El segmento correspondiente a la intersección está comprendido en la parte común a los dos triángulos, esto es, La intersección de IJ con el contorno del triángulo rojo.

Intersección de distintos elementos
Intersección de recta y cono. Se coge un punto cualquiera P sobre la recta y se une con V. La intersección de VP con la base del cono (plano azul) es P’.
Se une P’ con M (punto de intersección de la recta dada a con el plano azul donde se apoya el cono) obteniendo la recta g.
Las rectas g a determinan el plano de corte que pasa por V.
Si unimos los puntos de intersección de g con la base del cono (D’ C’) con V obtenemos DC en la intersección con a. DC son los puntos de intersección de a con el cono.

En diédrico. Uniendo V1 con P1 (punto aleatorio de la recta azul) obtenemos T2 en el alzado, lo bajamos con una vertical a la planta y obtenemos T1sobre la recta V- P1.
T1-B1 es la recta transformada de B1-P1 por proyección desde V.
B1-T1 corta a la base del cono en H1 K1. Estos puntos se unen con V1 obteniendo en la intersección con B1-P1 los puntos de intersección de la recta con el cono.
La superficie rayada es la sección del plano que pasa por la recta y por el vértice del cono V.

Para calcular la intersección de una recta m con una pirámide se puede hacer un plano vertical v que pase por la recta y que corta a la figura según el polígono abc. La intersección del polígono y la recta determina la intersección de la recta m y la pirámide.

Se puede operar en sistema diédrico como se hizo en el ejercicio del cono:
Uniendo V1 con T1 (punto aleatorio de la recta dada) obtenemos I2 en el alzado, lo bajamos con una vertical a la planta y obtenemos I1sobre la recta V1- T1.
P1-I1 es la recta transformada de T1-P1 por proyección desde V.
P1-I1 corta a la base del cono en N1 M1. Estos puntos se unen con V1 obteniendo en la intersección con T1-P1 los puntos de intersección de la recta A1 B1 con la pirámide.
La superficie rayada es la sección del plano que pasa por la recta y por el vértice del cono V.

La intersección de una recta y una pirámide. Como el plano es proyectante vertical (de canto), la traza vertical del plano determina en su intersección con las aristas de la pirámide los puntos de corte en el alzado. Estos puntos se bajan a la planta para dibujar el triángulo de sección. En los dos puntos de corte del triángulo con la línea dada tenemos la intersección con la figura.

Un plano vertical corta a la figura en planta en los puntos MNÑO, se suben al alzado y en la intersección del polígono que forman con la recta dad tenemos los puntos de entrada y salida de la recta en la figura.

Un plano horizontal corta a la figura según una sección idéntica a la base de la figura, ya que el prisma se forma por desplazamiento o extrusión de la base. Los puntos de corte obtenidos en alzado se bajan a la vista en planta obteniendo la forma idéntica a la base.

La intersección de una recta b con un prisma se puede obtener al trazar por un punto cualquiera del mismo Y una paralela a la dirección del eje del prisma (recta a).
La recta a corta en el alzado en P2, se baja a la planta (P1). Unimos P1 con B1 (intersección de b con el plano de la planta). P1-B1 corta a la base de la figura en dos puntos por los que se trazan paralelas a la recta a. La intersección de las paralelas con b define los puntos MN, puntos de intersección de la recta con el prisma.

El procedimiento para calcular la intersección de una recta con una figura es trazar por un punto de ella una recta a paralela a la dirección b de la figura. Donde la recta a corta al plano del suelo se une con el punto de intersección de la recta con el suelo. En los puntos de corte de esta recta con la base de la figura hacemos dos rectas de dirección b que cortan a la recta dada en los puntos de corte buscados.

La intersección de cualquier figura plana con una recta se puede obtener como intersección de la recta con la sección plana que produce el plano que incide en la recta.

Intersección de superficies radiadas
Para hallar la intersección de dos superficies que se cortan, se coge un plano auxiliar, este plano corta a las dos superficies en dos curvas planas, la intersección de las dos curvas planas nos da los puntos de intersección de la superficies por ese plano. Para calcular nuevos puntos de la intersección hay que pasar nuevos planos cortantes por las dos superficies.
Es una condición necesaria pasar los planos de forma que seccionen a las superficies en curvas fáciles de dibujar.

Existen distintos casos en la intersección de superficies, éstos se pueden clasificar en:
1- Mordedura. (M) En la intersección por mordedura cada superficie corta en parte a la otra, por regla general la curva de intersección es alabeada, que quiere decir que sus puntos no están sobre un plano.
2-Penetración. (P) En la penetración una superficie entra dentro de la otra y la atraviesa completamente, hay por tanto una curva de entrada y otra de salida.
3-Penetración tangencial. (PT) Se da cuando las dos curvas de entrada y salida de la superficie son tangentes en un punto. Si trazamos las dos rectas tangentes a las curvas por ese punto determinamos un plano que es tangente a las dos superficies.
4-Penetración máxima, (PM) las curvas de intersección de entrada y salida tienen dos puntos en común, con lo que se penetran recíprocamente.
Mordedura:
La intersección de dos figuras de ejes que se cruzan se obtiene trazando por el vértice V de una de ellas una paralela “a” a la dirección de la otra. Por a trazaremos distintos planos que corten a las dos figuras, así, el plano que pasa por a y es tangente al cilindro corta a las dos figuras según las rectas b c. Donde el plano d-a corta a la base de la figura: en N hacemos rectas paralelas (b) a la recta a sobre el cilindro. En Ñ unimos los puntos de la base del cono con su vértice V.
La intersección de b c es O, punto de la curva de intersección de las dos superficies. Si trazamos dos planos tangentes a las superficies por b y c se cortan en una recta tangente a las dos en el punto de intersección O.

En sistema diédrico hacemos la recta a por el vértice del cono V. Desde a hacemos planos que corten a las dos figuras. En los puntos de corte de las trazas de esos planos con la base del cilindro (TS), hacemos paralelas a la dirección del cilindro. Donde corte a la base del cono los unimos con el vértice V. La intersección de las rectas produce puntos de la curva de intersección de ambas superficies.

Penetración
El procedimiento es el mismo que el anterior. Por V seguimos la dirección q. Los planos que pasan por q cortan por lo general a las dos superficies en 4 rectas: hujk.
La intersección de uj es T, la de jh es s, la de kh es L, etc.
Los planos de corte que pasan por q seccionan al cilindro siempre mediante generatrices del mismo, esto es, rectas paralelas a su eje. Los planos de corte que pasan por q seccionan al cono siempre mediante generatrices del mismo, esto es, rectas que pasan por su vértice.

Como ejemplo se ha proyectado en diédrico un alzado y perfil y se ha pasado un plano ortogonal al perfil. La dirección del cilindro es una paralela al eje por N2, la del cono es una recta que pasa por M2 hasta el vértice A. La intersección de estas dos direcciones generan el punto V.

Intersección de superficies de revolución de ejes coplanares
Para calcular la intersección de superficies de revolución de ejes a b que se cortan podemos coger esferas que corten a ambas.
La esfera amarilla e cuyo centro C es la intersección de los ejes corta al hiperboloide gris según un plano cuya proyección es la recta r y al pequeño hiperboloide rosa según un plano cuya proyección es la recta z. La intersección de z y r genera una recta cuya proyección es el punto N, punto de la curva de intersección de ambas superficies.

Por regla general para calcular la intersección entre dos superficies se pasa un plano que corte a ambas produciendo dos curvas de intersección. La intersección de esas dos curvas genera 2 puntos de intersección de las dos superficies. Para calcular otros 2 pasamos otro plano paralelo al anterior procediendo de igual forma. Cada plano generará siempre 2 puntos de intersección y la curva pasará por el conjunto de todos los puntos de los planos que seccionan a las dos figuras.
Intersección de una esfera y un prisma recto. Un prisma recto cuyo eje pasa por el centro de la esfera genera como intersección entre los dos cuerpos una figura cuya planta es un cuadrado y cuyo alzado tiene cuatro circunferencias.
Una vista auxiliar muestra que la intersección de los dos sólidos produce una circunferencia concéntrica al contorno de la esfera.
Un objeto formado por la intersección de dos cilindros de igual diámetro tiene por proyecciones en planta y alzado circunferencias, mientras que en el perfil se percibe la intersección de los dos cilindros de ejes ortogonales entre sí como diagonales de un cuadrado que es el contorno de la figura.

Intersección de las dos superficies cilíndricas del mismo diámetro y de ejes ortogonales del ejercicio anterior y al mismo tiempo de una superficie prismática hexagonal con el eje perpendicular a ambas.

En la figura podemos observar la intersección de un cubo con dos toros. El toro de sección diametral menor provoca en su intersección una “lemniscata” deformada. Mientras que el toro de mayor sección es cortado por un plano tangente a las dos circunferencias de un perfil de la figura, por lo que la intersección del plano y el toro genera dos circunferencias secantes llamadas de Villarceau por ser quien las descubrió por el año 1840, como se puede percibir en la vista auxiliar del perfil proyectado A.

En la figura observamos distintas secciones del toro, en verde la figura parecida a una elipse alargada, en azul la lemniscata (inversa de la hipérbola) y en rosa la sección correspondiente a un plano tangente en el alzado a las dos circunferencias de los extremos de la figura, que genera como sección las dos circunferencias secantes de Villarceau.

Para calcular la intersección de un toro con un plano horizontal hacemos un plano vertical en planta de manera que produce como sección la circunferencia a1. Esta circunferencia se proyecta en el alzado desde el punto N1, que es donde corta a la circunferencia meridiana.
En el alzado la circunferencia a2 corta al extremo de la pieza en el punto P2. Desde el punto P2 bajamos una vertical hasta que corte a la circunferencia a1 en P1.
P1 es un punto de la curva sección del toro con forma de infinito llamada lemniscata de Bernoulli.
Para calcular la intersección del cono con los dos cilindros, se hacen dos secciones planas en el alzado m n. Éstas secciones son dos circunferencias que proyectamos a la planta. La intersección de estas dos circunferencias con el contorno de los dos cilindros genera P1 R1 que proyectamos al alzado y en la intersección con las circunferencias m n, respectivamente, obtenemos P2 R2, puntos de de intersección de la curva.
Para calcular la intersección del cono y cilindro se hace en el alzado una generatriz que va del vértice V2 al punto P2 de la circunferencia de la base. Ésta generatriz corta en el alzado al cilindro en el punto I2 desde el que hacemos una vertical que corta a la generatriz en la planta en el punto I1. Para obtener más puntos, de forma análoga se hacen nuevas generatrices hasta la base y donde corte de la circunferencia en el alzado se baja el punto de intersección hasta que corte a la generatriz en la planta.
Para calcular la intersección del cono y cilindro hacemos un plano horizontal que corta en el alzado al cono según una circunferencia azul, ésta determina en la intersección con el cilindro M2 N2 en el alzado. Se bajan dos rectas verticales a b hasta que corte en la proyección en planta de la circunferencia sección del cono en los puntos M1 N1. Estos puntos corresponden a la curva de intersección del cilindro y el cono. Para obtener nuevos puntos se hacen nuevos planos horizontales que corten al cono en la proyección vertical, en cuyos puntos se bajan verticales hasta que corten a la circunferencia sección de la proyección horizontal.
Para calcular la intersección de la esfera con el cilindro hacemos planos horizontales que cortan en el alzado a las esferas según circunferencias cuyas proyecciones son las rectas a 2 b2.
Las circunferencias de sección en planta cortan al cilindro en los puntos P1 R1, en cuyas verticales determinan en el alzado con la intersección de a2 b2, puntos de la curva de intersección del cilindro y la esfera.
Para calcular la intersección de un toro y un cilindro pasamos un plano horizontal que corta al toro en el alzado según las circunferencias amarilla y azul. Estas circunferencias se proyectan en planta mediante la corona circular comprendida entre los puntos N1 M1. En el perfil observamos que el cilindro corta al toro en el punto A3 que proyectamos a la planta obteniendo el punto A1, este es un punto de la intersección del cilindro con el toro. Para obtener otro punto en la misma recta paralela a la línea de tierra que pasa por el punto A1 observamos que corta a la circunferencia azul en el punto B1.

Intersecciones de figuras aplicando la diferencia entre ellas. La ventaja que tiene aplicar la diferencia entre dos figuras que se intersecan es que permite ver la inscripción de una otra sin necesidad de que aparezcan ambas de forma manifiesta.
En la figura se ha calculado la diferencia entre un dodecaedro regular y un cubo. De esta forma se ve una posible inscripción del cubo dentro del dodecaedro en la que los vértices del cubo ABCD coinciden con vértices del dodecaedro regular.
En cada arista del cubo se apoyan las diagonales de cada pentágono regular del dodecaedro.
Al practicar el hueco cúbico dentro del dodecaedro, como las aristas del cubo inciden en las diagonales de los pentágonos, esto es, en el dodecaedro regular, se tiene que las aristas del cubo son vistas de forma continua en las proyecciones diédricas.
Como el hueco cúbico corta las caras y vértices del dodecaedro, tenemos que el dodecaedro se transforma en seis prismas en forma de tejados a cuatro aguas.
Se han practicado dos cortes en la figura que dejan mostrar el interior de los lados del cubo, en el corte B-B el plano pasa por la diagonal del cubo. En el corte C-C EL plano es paralelo a una arista del cubo.

En este ejercicio se ha practicado la diferencia de un dodecaedro regular y una esfera, ambos concéntricos. Como el dodecaedro regular es un poliedro regular se tiene que todos los vértices equidistan del centro y como toda sección de la esfera por un plano es una circunferencia, se tiene que cada cara del dodecaedro regular tendrá un hueco centrado en forma de circunferencia.
Las tres vistas del dodecaedro en planta, alzado y perfil son iguales aunque giradas 90º. La vista auxiliar en la dirección B genera una cara del poliedro en verdadera magnitud. Para calcular la excentricidad de las elipses de las caras alternas, en la proyección DD se dibuja la esfera y se marcan los puntos de corte MN sobre el poliedro. Estos puntos se proyectan sobre la vista auxiliar B. La distancia MN sobre esta vista es el eje menor de la elipse, mientras que el mayor (en rojo) es igual al diámetro de la circunferencia en verdadera magnitud (en verde).
Sabemos que un plano que tiene una pendiente de 63,43° y sobre el mismo se proyecta una circunferencia se transforma en una elipse con esta relación entre sus ejes; de igual forma 58,28º genera una elipse como la de la cara amarilla, un plano de pendiente de 31,72° genera en el perfil una elipse como la de la cara naranja, etc.

Dado un cubo en el que se da en la proyección en planta S1 con un cono y una esfera huecos. La base del cono es tangente al lado del cuadrado en el que se apoya y las semiesfera tiene por diámetro mayor una circunferencia tangente a otro lado del cuadrado. Se trata de calcular la intersección de ambos huecos dentro de la figura.
Se hace una vista auxiliar A de la figura en planta S1 que va a ser la nueva planta y hacemos otra vista B proyectada de la figura, que corresponde a un nuevo alzado.
Dibujamos sobre la vista A un plano de corte perpendicular al eje del cono que secciona a la esfera y el cono según dos circunferencias de diámetros m1 x1, respectivamente.
Construimos la proyección en el alzado de las dos circunferencias que corresponden a estos diámetros por los centros respectivos del cono y de la semiesfera sobre esa vista. Estas dos circunferencias se cortan en un par de puntos que son los puntos de la intersección de la curva, por ejemplo el punto P2, que proyectamos sobre la planta y obtenemos su proyección P1.
Para obtener nuevos puntos de la curva se siguen haciendo planos perpendiculares al eje del cono que cortan nuevamente a las dos figuras según dos circunferencias en cuyos puntos de intersección tenemos más puntos de la curva.
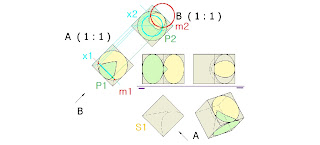
En la figura podemos observar tres vistas de la pieza en planta, alzado y perfil y otras dos nuevas vistas en diédrico con una posición oblicua del cubo. Tenemos una última proyección axonométrica de la figura en la que se percibe la intersección de las semiesfera hueca con el cono hueco dentro del cubo.

 En la figura observamos la intersección de un cono y de un cilindro, por uno de los lados tenemos un caso sencillo de una hipérbola, ya que es la intersección de un plano vertical correspondiente a la base del cilindro con el cono. Por otro lado tenemos la intersección de la superficie cilíndrica con la cónica, que genera una curva alabeada.
En la figura observamos la intersección de un cono y de un cilindro, por uno de los lados tenemos un caso sencillo de una hipérbola, ya que es la intersección de un plano vertical correspondiente a la base del cilindro con el cono. Por otro lado tenemos la intersección de la superficie cilíndrica con la cónica, que genera una curva alabeada.
Para calcular la intersección de ambas superficies pasamos planos horizontales que cortan ambas figuras, en el caso del cono la sección de cada plano es una circunferencia y en el del cilindro son dos rectas de punta. La intersección de cada circunferencia con cada par de rectas determina los puntos de intersección de la superficie cilíndrica y cónica. Como ejemplo podemos observar la intersección de la circunferencia m con la recta de punta t determina B, punto de intersección de la curva alabeada de ambas superficies.

Podemos observar un cono al que se le han restado otros dos conos, uno de ellos tiene el eje en el mismo plano que el cono dado, mientras que el otro lo tiene paralelo.



Los dos planos g j se cortan en una recta a que pasa por el segundo, tercero y cuarto cuadrante. Para determinar la intersección de ambos, prolongamos las trazas horizontales de ambos y obtenemos el punto de intersección P sobre el plano horizontal.
Prolongamos las trazas verticales de los planos hasta que se cortan en el punto O sobre el plano vertical. La recta que pasa por ambos puntos es la de intersección de los dos planos. Si representamos la tercera proyección en el perfil podemos observar que la intersección de las dos trazas determina M. Los 3 puntos POM, por pertenecer a ambos planos y estar en la recta de intersección están alineados.

Tenemos los dos planos g j de color azul determinados por las trazas g1 g2 j1 j2. Prolongamos la traza horizontal g1 del plano g hasta que corta a la traza horizontal j1 del plano j, obteniendo un punto de intersección P1 sobre el plano horizontal.
Prolongamos las trazas verticales de ambos planos g2 j2 y en su intersección O2 obtenemos un punto de la recta de intersección a sobre el plano vertical. Este punto O2 lo proyectamos sobre el perfil obteniendo O3.
Tenemos que la recta pasa sobre el plano horizontal por P1 y por el plano vertical por O2, proyectamos estos puntos sobre la línea de tierra obtenemos P2 O2, respectivamente. Los proyectamos también sobre el perfil para obtener la tercera proyección de los mismos P3 O3. La recta de intersección en su proyección horizontal a1 pasa por los puntos P1 O1, en su proyección vertical pasa por los puntos P2 O2. En su proyección en el perfil pasa por O3 y por el punto final del segmento d2, que es igual al alejamiento d1, esto es, la distancia del punto P1 al plano vertical.
De esta manera tenemos las tres proyecciones de la recta a (en el dibujo aparecen en color rojo), recta que pasa por el segundo, tercero y cuarto cuadrante.
Intersección de 2 figuras planas
Para calcular la intersección de dos triángulos se hace uso de un plano auxiliar horizontal alfa que los corta según las rectas a b, la intersección M de a b es un punto de la línea de intersección de los dos triángulos.

Operando de igual forma con otro plano beta, corta a los triángulos en c d , la intersección de c d es N.
MN es por tanto la recta de intersección de los dos planos.

El plano horizontal de mayor cota corta al triángulo amarillo según AB, al rojo según MN, la intersección de AB y MN es I. Bajamos las proyecciones de A2, B2, M2,…al contorno de los triángulos en planta, obteniendo A1, B1,…etc.
El plano horizontal de menor cota corta al triángulo amarillo según KL, al rojo según YZ, la intersección de KL e YZ es J. Bajamos igualmente las proyecciones de estos puntos a la planta.
La recta YJ es la intersección de los dos triángulos. El segmento correspondiente a la intersección está comprendido en la parte común a los dos triángulos, esto es, La intersección de IJ con el contorno del triángulo rojo.

Intersección de distintos elementos
Intersección de recta y cono. Se coge un punto cualquiera P sobre la recta y se une con V. La intersección de VP con la base del cono (plano azul) es P’.
Se une P’ con M (punto de intersección de la recta dada a con el plano azul donde se apoya el cono) obteniendo la recta g.
Las rectas g a determinan el plano de corte que pasa por V.
Si unimos los puntos de intersección de g con la base del cono (D’ C’) con V obtenemos DC en la intersección con a. DC son los puntos de intersección de a con el cono.

En diédrico. Uniendo V1 con P1 (punto aleatorio de la recta azul) obtenemos T2 en el alzado, lo bajamos con una vertical a la planta y obtenemos T1sobre la recta V- P1.
T1-B1 es la recta transformada de B1-P1 por proyección desde V.
B1-T1 corta a la base del cono en H1 K1. Estos puntos se unen con V1 obteniendo en la intersección con B1-P1 los puntos de intersección de la recta con el cono.
La superficie rayada es la sección del plano que pasa por la recta y por el vértice del cono V.

Para calcular la intersección de una recta m con una pirámide se puede hacer un plano vertical v que pase por la recta y que corta a la figura según el polígono abc. La intersección del polígono y la recta determina la intersección de la recta m y la pirámide.

Se puede operar en sistema diédrico como se hizo en el ejercicio del cono:
Uniendo V1 con T1 (punto aleatorio de la recta dada) obtenemos I2 en el alzado, lo bajamos con una vertical a la planta y obtenemos I1sobre la recta V1- T1.
P1-I1 es la recta transformada de T1-P1 por proyección desde V.
P1-I1 corta a la base del cono en N1 M1. Estos puntos se unen con V1 obteniendo en la intersección con T1-P1 los puntos de intersección de la recta A1 B1 con la pirámide.
La superficie rayada es la sección del plano que pasa por la recta y por el vértice del cono V.

La intersección de una recta y una pirámide. Como el plano es proyectante vertical (de canto), la traza vertical del plano determina en su intersección con las aristas de la pirámide los puntos de corte en el alzado. Estos puntos se bajan a la planta para dibujar el triángulo de sección. En los dos puntos de corte del triángulo con la línea dada tenemos la intersección con la figura.

Un plano vertical corta a la figura en planta en los puntos MNÑO, se suben al alzado y en la intersección del polígono que forman con la recta dad tenemos los puntos de entrada y salida de la recta en la figura.

Un plano horizontal corta a la figura según una sección idéntica a la base de la figura, ya que el prisma se forma por desplazamiento o extrusión de la base. Los puntos de corte obtenidos en alzado se bajan a la vista en planta obteniendo la forma idéntica a la base.

La intersección de una recta b con un prisma se puede obtener al trazar por un punto cualquiera del mismo Y una paralela a la dirección del eje del prisma (recta a).
La recta a corta en el alzado en P2, se baja a la planta (P1). Unimos P1 con B1 (intersección de b con el plano de la planta). P1-B1 corta a la base de la figura en dos puntos por los que se trazan paralelas a la recta a. La intersección de las paralelas con b define los puntos MN, puntos de intersección de la recta con el prisma.

El procedimiento para calcular la intersección de una recta con una figura es trazar por un punto de ella una recta a paralela a la dirección b de la figura. Donde la recta a corta al plano del suelo se une con el punto de intersección de la recta con el suelo. En los puntos de corte de esta recta con la base de la figura hacemos dos rectas de dirección b que cortan a la recta dada en los puntos de corte buscados.

La intersección de cualquier figura plana con una recta se puede obtener como intersección de la recta con la sección plana que produce el plano que incide en la recta.

Intersección de superficies radiadas
Para hallar la intersección de dos superficies que se cortan, se coge un plano auxiliar, este plano corta a las dos superficies en dos curvas planas, la intersección de las dos curvas planas nos da los puntos de intersección de la superficies por ese plano. Para calcular nuevos puntos de la intersección hay que pasar nuevos planos cortantes por las dos superficies.
Es una condición necesaria pasar los planos de forma que seccionen a las superficies en curvas fáciles de dibujar.

Existen distintos casos en la intersección de superficies, éstos se pueden clasificar en:
1- Mordedura. (M) En la intersección por mordedura cada superficie corta en parte a la otra, por regla general la curva de intersección es alabeada, que quiere decir que sus puntos no están sobre un plano.
2-Penetración. (P) En la penetración una superficie entra dentro de la otra y la atraviesa completamente, hay por tanto una curva de entrada y otra de salida.
3-Penetración tangencial. (PT) Se da cuando las dos curvas de entrada y salida de la superficie son tangentes en un punto. Si trazamos las dos rectas tangentes a las curvas por ese punto determinamos un plano que es tangente a las dos superficies.
4-Penetración máxima, (PM) las curvas de intersección de entrada y salida tienen dos puntos en común, con lo que se penetran recíprocamente.
Mordedura:
La intersección de dos figuras de ejes que se cruzan se obtiene trazando por el vértice V de una de ellas una paralela “a” a la dirección de la otra. Por a trazaremos distintos planos que corten a las dos figuras, así, el plano que pasa por a y es tangente al cilindro corta a las dos figuras según las rectas b c. Donde el plano d-a corta a la base de la figura: en N hacemos rectas paralelas (b) a la recta a sobre el cilindro. En Ñ unimos los puntos de la base del cono con su vértice V.
La intersección de b c es O, punto de la curva de intersección de las dos superficies. Si trazamos dos planos tangentes a las superficies por b y c se cortan en una recta tangente a las dos en el punto de intersección O.

En sistema diédrico hacemos la recta a por el vértice del cono V. Desde a hacemos planos que corten a las dos figuras. En los puntos de corte de las trazas de esos planos con la base del cilindro (TS), hacemos paralelas a la dirección del cilindro. Donde corte a la base del cono los unimos con el vértice V. La intersección de las rectas produce puntos de la curva de intersección de ambas superficies.

Penetración
El procedimiento es el mismo que el anterior. Por V seguimos la dirección q. Los planos que pasan por q cortan por lo general a las dos superficies en 4 rectas: hujk.
La intersección de uj es T, la de jh es s, la de kh es L, etc.
Los planos de corte que pasan por q seccionan al cilindro siempre mediante generatrices del mismo, esto es, rectas paralelas a su eje. Los planos de corte que pasan por q seccionan al cono siempre mediante generatrices del mismo, esto es, rectas que pasan por su vértice.

Como ejemplo se ha proyectado en diédrico un alzado y perfil y se ha pasado un plano ortogonal al perfil. La dirección del cilindro es una paralela al eje por N2, la del cono es una recta que pasa por M2 hasta el vértice A. La intersección de estas dos direcciones generan el punto V.

Intersección de superficies de revolución de ejes coplanares
Para calcular la intersección de superficies de revolución de ejes a b que se cortan podemos coger esferas que corten a ambas.
La esfera amarilla e cuyo centro C es la intersección de los ejes corta al hiperboloide gris según un plano cuya proyección es la recta r y al pequeño hiperboloide rosa según un plano cuya proyección es la recta z. La intersección de z y r genera una recta cuya proyección es el punto N, punto de la curva de intersección de ambas superficies.

Por regla general para calcular la intersección entre dos superficies se pasa un plano que corte a ambas produciendo dos curvas de intersección. La intersección de esas dos curvas genera 2 puntos de intersección de las dos superficies. Para calcular otros 2 pasamos otro plano paralelo al anterior procediendo de igual forma. Cada plano generará siempre 2 puntos de intersección y la curva pasará por el conjunto de todos los puntos de los planos que seccionan a las dos figuras.
Intersección de una esfera y un prisma recto. Un prisma recto cuyo eje pasa por el centro de la esfera genera como intersección entre los dos cuerpos una figura cuya planta es un cuadrado y cuyo alzado tiene cuatro circunferencias.
Una vista auxiliar muestra que la intersección de los dos sólidos produce una circunferencia concéntrica al contorno de la esfera.

Un objeto formado por la intersección de dos cilindros de igual diámetro tiene por proyecciones en planta y alzado circunferencias, mientras que en el perfil se percibe la intersección de los dos cilindros de ejes ortogonales entre sí como diagonales de un cuadrado que es el contorno de la figura.

Intersección de las dos superficies cilíndricas del mismo diámetro y de ejes ortogonales del ejercicio anterior y al mismo tiempo de una superficie prismática hexagonal con el eje perpendicular a ambas.

En la figura podemos observar la intersección de un cubo con dos toros. El toro de sección diametral menor provoca en su intersección una “lemniscata” deformada. Mientras que el toro de mayor sección es cortado por un plano tangente a las dos circunferencias de un perfil de la figura, por lo que la intersección del plano y el toro genera dos circunferencias secantes llamadas de Villarceau por ser quien las descubrió por el año 1840, como se puede percibir en la vista auxiliar del perfil proyectado A.

En la figura observamos distintas secciones del toro, en verde la figura parecida a una elipse alargada, en azul la lemniscata (inversa de la hipérbola) y en rosa la sección correspondiente a un plano tangente en el alzado a las dos circunferencias de los extremos de la figura, que genera como sección las dos circunferencias secantes de Villarceau.

Para calcular la intersección de un toro con un plano horizontal hacemos un plano vertical en planta de manera que produce como sección la circunferencia a1. Esta circunferencia se proyecta en el alzado desde el punto N1, que es donde corta a la circunferencia meridiana.
En el alzado la circunferencia a2 corta al extremo de la pieza en el punto P2. Desde el punto P2 bajamos una vertical hasta que corte a la circunferencia a1 en P1.
P1 es un punto de la curva sección del toro con forma de infinito llamada lemniscata de Bernoulli.

Para calcular la intersección del cono con los dos cilindros, se hacen dos secciones planas en el alzado m n. Éstas secciones son dos circunferencias que proyectamos a la planta. La intersección de estas dos circunferencias con el contorno de los dos cilindros genera P1 R1 que proyectamos al alzado y en la intersección con las circunferencias m n, respectivamente, obtenemos P2 R2, puntos de de intersección de la curva.

Para calcular la intersección del cono y cilindro se hace en el alzado una generatriz que va del vértice V2 al punto P2 de la circunferencia de la base. Ésta generatriz corta en el alzado al cilindro en el punto I2 desde el que hacemos una vertical que corta a la generatriz en la planta en el punto I1. Para obtener más puntos, de forma análoga se hacen nuevas generatrices hasta la base y donde corte de la circunferencia en el alzado se baja el punto de intersección hasta que corte a la generatriz en la planta.

Para calcular la intersección del cono y cilindro hacemos un plano horizontal que corta en el alzado al cono según una circunferencia azul, ésta determina en la intersección con el cilindro M2 N2 en el alzado. Se bajan dos rectas verticales a b hasta que corte en la proyección en planta de la circunferencia sección del cono en los puntos M1 N1. Estos puntos corresponden a la curva de intersección del cilindro y el cono. Para obtener nuevos puntos se hacen nuevos planos horizontales que corten al cono en la proyección vertical, en cuyos puntos se bajan verticales hasta que corten a la circunferencia sección de la proyección horizontal.

Para calcular la intersección de la esfera con el cilindro hacemos planos horizontales que cortan en el alzado a las esferas según circunferencias cuyas proyecciones son las rectas a 2 b2.
Las circunferencias de sección en planta cortan al cilindro en los puntos P1 R1, en cuyas verticales determinan en el alzado con la intersección de a2 b2, puntos de la curva de intersección del cilindro y la esfera.

Para calcular la intersección de un toro y un cilindro pasamos un plano horizontal que corta al toro en el alzado según las circunferencias amarilla y azul. Estas circunferencias se proyectan en planta mediante la corona circular comprendida entre los puntos N1 M1. En el perfil observamos que el cilindro corta al toro en el punto A3 que proyectamos a la planta obteniendo el punto A1, este es un punto de la intersección del cilindro con el toro. Para obtener otro punto en la misma recta paralela a la línea de tierra que pasa por el punto A1 observamos que corta a la circunferencia azul en el punto B1.

Intersecciones de figuras aplicando la diferencia entre ellas. La ventaja que tiene aplicar la diferencia entre dos figuras que se intersecan es que permite ver la inscripción de una otra sin necesidad de que aparezcan ambas de forma manifiesta.
En la figura se ha calculado la diferencia entre un dodecaedro regular y un cubo. De esta forma se ve una posible inscripción del cubo dentro del dodecaedro en la que los vértices del cubo ABCD coinciden con vértices del dodecaedro regular.
En cada arista del cubo se apoyan las diagonales de cada pentágono regular del dodecaedro.
Al practicar el hueco cúbico dentro del dodecaedro, como las aristas del cubo inciden en las diagonales de los pentágonos, esto es, en el dodecaedro regular, se tiene que las aristas del cubo son vistas de forma continua en las proyecciones diédricas.
Como el hueco cúbico corta las caras y vértices del dodecaedro, tenemos que el dodecaedro se transforma en seis prismas en forma de tejados a cuatro aguas.
Se han practicado dos cortes en la figura que dejan mostrar el interior de los lados del cubo, en el corte B-B el plano pasa por la diagonal del cubo. En el corte C-C EL plano es paralelo a una arista del cubo.

En este ejercicio se ha practicado la diferencia de un dodecaedro regular y una esfera, ambos concéntricos. Como el dodecaedro regular es un poliedro regular se tiene que todos los vértices equidistan del centro y como toda sección de la esfera por un plano es una circunferencia, se tiene que cada cara del dodecaedro regular tendrá un hueco centrado en forma de circunferencia.
Las tres vistas del dodecaedro en planta, alzado y perfil son iguales aunque giradas 90º. La vista auxiliar en la dirección B genera una cara del poliedro en verdadera magnitud. Para calcular la excentricidad de las elipses de las caras alternas, en la proyección DD se dibuja la esfera y se marcan los puntos de corte MN sobre el poliedro. Estos puntos se proyectan sobre la vista auxiliar B. La distancia MN sobre esta vista es el eje menor de la elipse, mientras que el mayor (en rojo) es igual al diámetro de la circunferencia en verdadera magnitud (en verde).
Sabemos que un plano que tiene una pendiente de 63,43° y sobre el mismo se proyecta una circunferencia se transforma en una elipse con esta relación entre sus ejes; de igual forma 58,28º genera una elipse como la de la cara amarilla, un plano de pendiente de 31,72° genera en el perfil una elipse como la de la cara naranja, etc.

Dado un cubo en el que se da en la proyección en planta S1 con un cono y una esfera huecos. La base del cono es tangente al lado del cuadrado en el que se apoya y las semiesfera tiene por diámetro mayor una circunferencia tangente a otro lado del cuadrado. Se trata de calcular la intersección de ambos huecos dentro de la figura.
Se hace una vista auxiliar A de la figura en planta S1 que va a ser la nueva planta y hacemos otra vista B proyectada de la figura, que corresponde a un nuevo alzado.
Dibujamos sobre la vista A un plano de corte perpendicular al eje del cono que secciona a la esfera y el cono según dos circunferencias de diámetros m1 x1, respectivamente.
Construimos la proyección en el alzado de las dos circunferencias que corresponden a estos diámetros por los centros respectivos del cono y de la semiesfera sobre esa vista. Estas dos circunferencias se cortan en un par de puntos que son los puntos de la intersección de la curva, por ejemplo el punto P2, que proyectamos sobre la planta y obtenemos su proyección P1.
Para obtener nuevos puntos de la curva se siguen haciendo planos perpendiculares al eje del cono que cortan nuevamente a las dos figuras según dos circunferencias en cuyos puntos de intersección tenemos más puntos de la curva.

En la figura podemos observar tres vistas de la pieza en planta, alzado y perfil y otras dos nuevas vistas en diédrico con una posición oblicua del cubo. Tenemos una última proyección axonométrica de la figura en la que se percibe la intersección de las semiesfera hueca con el cono hueco dentro del cubo.

 En la figura observamos la intersección de un cono y de un cilindro, por uno de los lados tenemos un caso sencillo de una hipérbola, ya que es la intersección de un plano vertical correspondiente a la base del cilindro con el cono. Por otro lado tenemos la intersección de la superficie cilíndrica con la cónica, que genera una curva alabeada.
En la figura observamos la intersección de un cono y de un cilindro, por uno de los lados tenemos un caso sencillo de una hipérbola, ya que es la intersección de un plano vertical correspondiente a la base del cilindro con el cono. Por otro lado tenemos la intersección de la superficie cilíndrica con la cónica, que genera una curva alabeada.Para calcular la intersección de ambas superficies pasamos planos horizontales que cortan ambas figuras, en el caso del cono la sección de cada plano es una circunferencia y en el del cilindro son dos rectas de punta. La intersección de cada circunferencia con cada par de rectas determina los puntos de intersección de la superficie cilíndrica y cónica. Como ejemplo podemos observar la intersección de la circunferencia m con la recta de punta t determina B, punto de intersección de la curva alabeada de ambas superficies.

Podemos observar un cono al que se le han restado otros dos conos, uno de ellos tiene el eje en el mismo plano que el cono dado, mientras que el otro lo tiene paralelo.

Para calcular la intersección de los dos conos que tienen ejes coplanarios, se hace una esfera f con el centro en la intersección de los ejes de los conos y que corta a ambos según dos circunferencias a b, cuya representación en el alzado son dos rectas que se cortan en un punto P, este punto es el de la curva de intersección de ambas superficies. Para determinar nuevos puntos se hace una esfera mayor o menor con el mismo centro que corta a ambos conos según dos circunferencias que se cortan en una recta cuya representación en el alzado es un punto, (por ser una recta de punta), y éste es un punto de la curva de intersección en el alzado.

Para calcular la intersección entre los dos conos de ejes de revolución paralelos, se pasan planos verticales que corten ambos en el alzado según dos circunferencias que se transforman en rectas. Proyectamos estas circunferencias sobre la planta y observamos en la intersección de las mismas un par de puntos de la intersección que son en realidad puntos de la curva de intersección de los dos conos. Éstos: se suben al alzado obteniendo la curva de intersección de ambas superficies, sobre el alzado son puntos coincidentes por ser rectas de punta, esto es, rectas perpendiculares al plano vertical.

Para calcular la intersección entre los dos conos de ejes de revolución paralelos, se pasan planos verticales que corten ambos en el alzado según dos circunferencias que se transforman en rectas. Proyectamos estas circunferencias sobre la planta y observamos en la intersección de las mismas un par de puntos de la intersección que son en realidad puntos de la curva de intersección de los dos conos. Éstos: se suben al alzado obteniendo la curva de intersección de ambas superficies, sobre el alzado son puntos coincidentes por ser rectas de punta, esto es, rectas perpendiculares al plano vertical.



No hay comentarios:
Publicar un comentario